Показатели дифференциации доходов населения.
Дифференциация доходов населения
- реально существующие различия в уровне доходов населения, в
значительной степени, предопределяющие социальную дифференциацию в
обществе, характер его социальной структуры. В странах с развитой
рыночной экономикой уровень дохода является одним из важнейших
конституирующих социальное положение признаков (наряду с собственностью,
отношением к власти и т. д.).
Неравенство доходов объясняется следующими причинами:
1) разными интеллектуальными и физическими способностями;
2) разным уровнем образования и профессиональной подготовки;
3) профессиональными вкусами и способностями к риску;
4) неравенством владения собственностью;
5) монополизмом на рынке товаров и услуг;
6) удачей, связями, несчастьями и дискриминацией.
Дифференциация
доходов, как правило, рассматривается по размеру среднедушевого
совокупного дохода населения в целом, отдельных регионов и групп
домохозяйств (проживающих в городской местности, в сельской местности,
из них хозяйств пенсионеров, имеющих детей до 16 лет т.д.
Широко
распространена оценка дифференциации доходов населения путем соотношения
групп населения с наибольшими и наименьшими доходами. Все население
разбивается при этом на равные по численности десяти-, двадцати или
двадцатипятипроцентные группы. После чего доход, полученный последней
группой, делят на доход, полученный первой группой. Соответственно
получают децильное, квинтильное или квартильное соотношение доходов
населения.
Дифференциация населения по доходам характеризуется
различными показателями: фондовым коэффициентом дифференциации
(коэффициент фондов), показателем дифференциации по квинтильным
(20-типроцентным) группам населения, коэффициентом концентрации доходов
(индексом Джинни), а также графически с помощью кривой Лоуренса.
Модальный и медианный
доходы - это важные структурные показатели, которые характеризуют
отклонение среднедушевого дохода от среднего значения для каждой группы.
Как правило, результаты исследований свидетельствуют, что одна половина
населения имеет доход ниже среднего, а вторая половина - выше среднего.
Широко распространен в статистических исследованиях по неравенству в распределении доходов децильный
коэффициент дифференциации доходов, который исчисляется как отношение
минимального дохода у 10% наиболее обеспеченных граждан к максимальному
доходу 10% наименее обеспеченных граждан.:
Коэффициент фондов Кф, с помощью которого измеряют различие между суммарными (средними) значениями доходов 10% наиболее обеспеченной (Ч10 ) и 10% наименее обеспеченной (Ч1) части населения.
Коэффициент концентрации доходов (индекс Джинни)
характеризует степень неравномерности распределения всей суммы доходов
между отдельными группами населения; его величина может варьироваться от
0 до 1, при этом, чем выше значение показателя, тем более неравномерно
распределены доходы в обществе.
где Li , Li-1 - доля населения в интервале; Si , Si-1 - доля суммарного дохода (на начало и конец i-го интервала).
Степень неравенства доходов определяется с помощью кривой Лоуренса.
На основе данных о распределении доходов население можно объединить в
определенные доходные группы. Сопоставив долю каждой из групп в
совокупном доходе, можно графически изобразить кривую, иллюстрирующую
дифференциацию доходов.
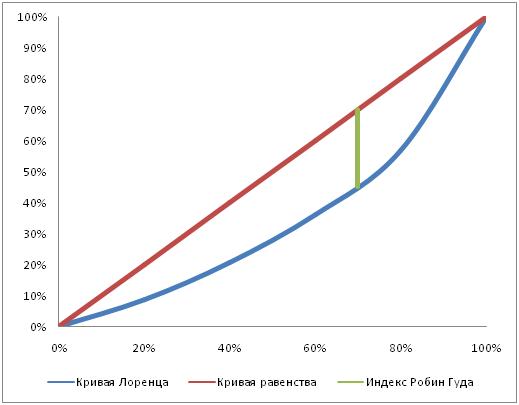
Кривая Лоренца — это графическое изображение функции распределения. Она была предложена американским экономистом Максом Отто Лоренцем в 1905 году как показатель неравенства в доходах населения.
В таком представлении она есть изображение функции распределения, в
котором аккумулируются доли численности и доходов населения. В
прямоугольной системе координат кривая Лоренца является выпуклой вниз и
проходит под диагональю единичного квадрата, расположенного в I
координатной четверти.
Каждая точка на кривой Лоренца соответствует утверждению вроде «20
самых бедных процентов населения получают всего 7 % дохода». В случае
равного распределения каждая группа населения имеет доход,
пропорциональный своей численности. Такой случай описывается кривой
равенства (line of perfect equality), являющейся прямой, соединяющей
начало координат и точку (1;1). В случае полного неравенства (когда лишь
один член общества имеет доход) кривая (line of perfect inequality)
сначала «прилипает» к оси абсцисс, а потом из точки (1;0) «взмывает» к
точке (1;1). Кривая Лоренца заключена между кривыми равенства и
неравенства.
Кривые Лоренца применяют для распределений не только доходов, но и
имущества домохозяйств, долей рынка для фирм в отрасли, природных
ресурсов по государствам. Встретить кривую Лоренца можно и за пределами
экономической науки. Из кривой Лоренца можно вывести коэффициент Джинни и индекс Робин Гуда.
Индекс Робин Гуда (Robin Hood index), также известный как индекс
Гувера (Hoover index), — это ещё один показатель неравенства по доходам,
имеющий связь с кривой Лоренца. Он равен той доле дохода общества,
которую необходимо перераспределить для достижения равенства. Графически
он представим как самый длинный вертикальный отрезок, соединяющий
фактическую кривую Лоренца с линией равенства (биссектрисой I
координатной четверти).
При абсолютной делимости дохода индекс Гувера принадлежит
полуоткрытому интервалу [0;1). Если же доход не делим до бесконечности,
то говорят о доле дохода, перераспределение которой максимально
приближает данное общество к равенству.
Индекс Робин Гуда широко используется в оценках обеспеченности
населённых районов врачами общей практики. При таких оценках кривая
Лоренца будет наполняться не доходами, а удельным числом врачей общей
практики на местность или группу людей, а ранжировать по данному
показателю следует не домохозяйства, а местности или группы людей. Таким
образом, он показывает, какую часть докторов следует перенаправить в
другие районы для поддержания равной обеспеченности медицинским
персоналом на всей исследуемой территории.
|

